Kolmogorov's Generalized Mean

By Kardi Teknomo, PhD .

< Previous | Next | Contents >

Generalized Mean

In the previous section, we have discussed two generalized means of Minkowski mean and Lehmer mean. However, the two means is not "general enough" because Minkowski mean does not have a specific p to represent Geometric mean while Lehmer mean does not have a specific p to indicate Quadratic mean. This lead to a question whether we have a general mean to represent all the four basic means (Arithmetic mean, Geometric mean, Harmonic Mean and Quadratic Mean).

Phillips (2000) suggests the following quasi-arithmetic generalized mean which has been available through the work of Andrey Kolmogorov in 1930 . The mean is quite general that it can cover arithmetic mean , quadratic mean , harmonic mean and geometric mean and many others. In fact, Kolmogorov Generalzed mean can also cover Minkowski mean as shown in the example below.

Instead of using a parameter, however, Kolmogorov generalized mean uses function and its inverse function to generate mean. Suppose we have a continuous monotonic function from positive real numbers to positive real number and the inverse function of exist, then we can make infinite number of means using

Extending the generalized mean to input numbers is straightforward.

I hope you remember the definition of inverse function that if then . Simple inverse function can be obtained by exchange and in the expression. Then the following are two properties of inverse function:

Example:

, then , then we have which is an arithmetic mean

Example:

, then , then we have which can be simplified into Geometric mean by Since only accept positive values of x, Geometric mean also can accept positive values.

Example:

, then , then we get which is a quadratic mean

Example:

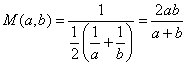, then , then we obtain which is a harmonic mean

Example:

, then , then we get which is Minkowski mean

Example:

, then , then we obtain which is a Harmonic mean

Table below provides the summary of functions to relate Kolmogorov generalized mean and other means.

< Previous | Next | Contents >

See also: Minkowski mean , Lehmer mean , arithmetic mean , harmonic mean , geometric mean , quadratic mean
Rate this tutorial or give your comments about this tutorial

This tutorial is copyrighted .

Preferable reference for this tutorial is

Teknomo, Kardi (2015) Mean and Average. https:\\people.revoledu.com\kardi\tutorial\BasicMath\Average\